Podem saber quan va sorgir el primer cas de covid-19?

Trobar el pacient zero, el primer cas de covid-19, és crucial per a esbrinar l’origen de la pandèmia. Saber on i per què va poder contraure la malaltia ens donarà les pistes necessàries per a evitar els riscs de focus futurs, reemergències i noves pandèmies. Per descomptat, cal preservar-ne la identitat per evitar culpabilitzar i estigmatitzar.

Com es traça l’origen d’una epidèmia

Qualsevol investigació de fets consumats, com si fóssim detectius policíacs, ens porta a mirar cap enrere per lligar caps. Disposem de la declaració de vint-i-set casos de pneumònia de causa desconeguda als serveis sanitaris de Wuhan el 31 de desembre de 2019, amb aparició de símptomes el dia 7 del mateix mes. Ara sabem que el període de latència pre-simptomàtica de la covid-19 és del voltant de dues setmanes, de manera que el primer cas ens podem aventurar a situar-lo el novembre del 2019.

Segurament no van aparèixer de cop i en tots els malalts alhora, sinó que s’hauria de pensar en dies enrere. El març del 2020 es deia que el primer cas podia haver sorgit a la província de Hubei el dia 17 de novembre de 2019.

Després de l’expansió a la Xina, el gener del 2020 van començar a aparèixer casos en hospitals a Europa, els Estats Units, Corea del Sud… Una altra dada a tenir en compte és el reconeixement a l’abril de l’any passat per part del Centre de Coordinació d’Alertes i Emergències Sanitàries de l’estat espanyol que quan es van detectar els primers casos a Espanya, el SARS-CoV-2 ja era entre nosaltres. Dada comprovada més tard mitjançant estudis de seqüenciació del material genètic del virus i del seu seguiment.

Fins ara han aparegut models de predicció per a trobar el pacient zero i situar i precisar l’origen del primer contagi. Un dels més nous ha estat publicat fa molt poc a la revista PLOS Pathogens en una col·laboració a tres bandes entre la Universitat de Kent (Regne Unit), Chicago (EUA) i el Centre de Biologia de la República Txeca.

Són fiables els models matemàtics per a descriure l’evolució d’una epidèmia?

Per poder comprendre aquesta nova investigació, primer hem de familiaritzar-nos amb els mètodes més emprats. Els models matemàtics juguen un paper important en el disseny de possibles estratègies de control de malalties en centrar-se en els aspectes clau d’aquestes, determinar el llindar per a la supervivència de la malaltia i avaluar l’efecte de les estratègies dissenyades, entre més aspectes.

La simulació bàsica és el model SIR, desenvolupat per Sir Ronald Ross i Anderson Gray McKendrick. Aquesta mena de models es basen en el fet que la població es pot classificar en tres grups compartimentats independents: individu susceptible (S), individu infectat (I) i individu recuperat (R). A partir d’aquest model, tant el nombre com el tipus de grup es poden modificar per reflectir el comportament de cada malaltia, com es mostra a la Figura 1.

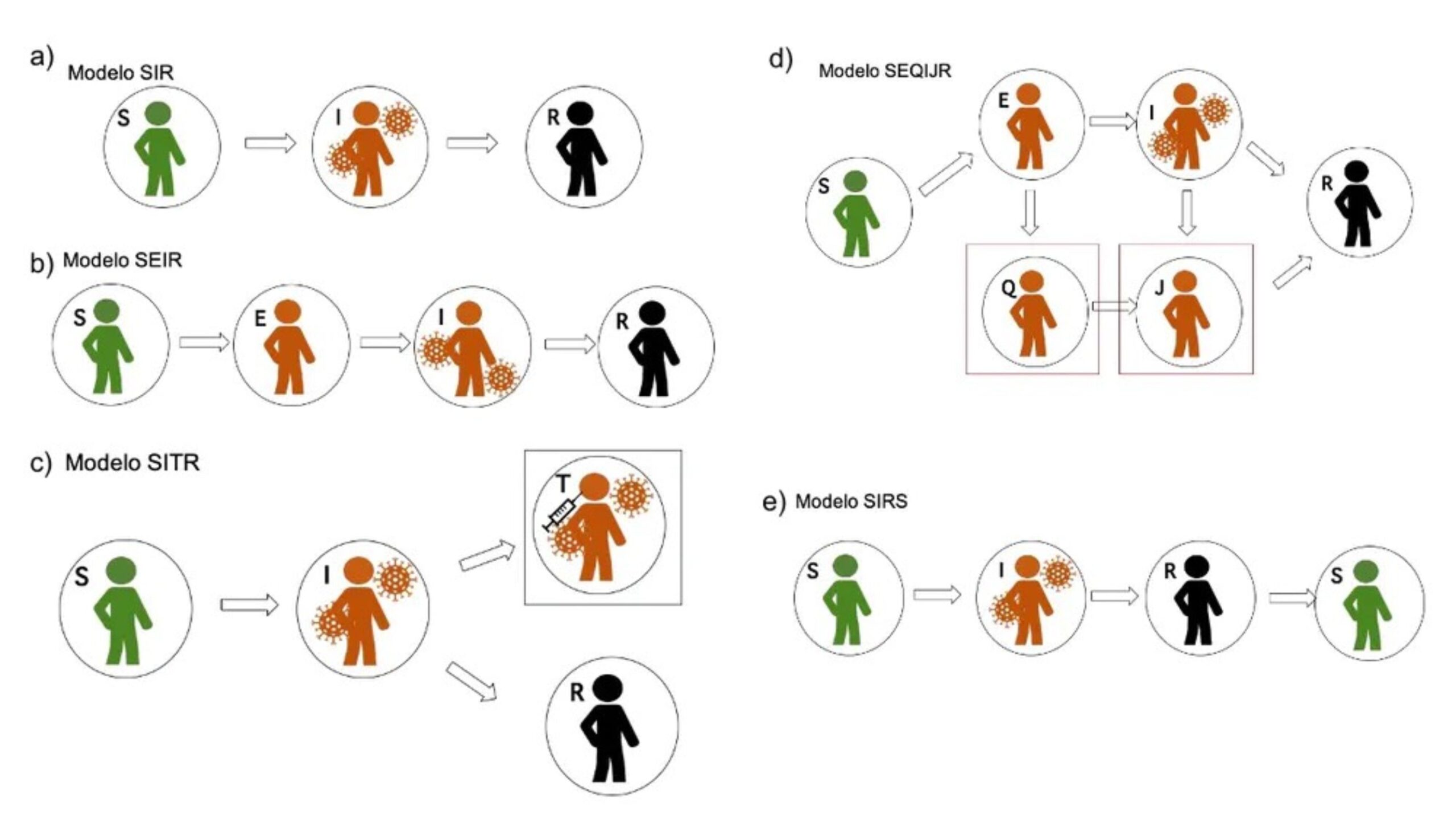
Per exemple, el model SEIR inclou un estat intermedi, individu exposat (E) amb el qual es mira de simular el període d’incubació. Al model SITR alguns individus són tractats (T), entenent per “tractats” aïllats o vaccinats, evitant així que generin possibles noves infeccions. Als models SIRS, que són els models endèmics que es fan servir per a malalties com ara la grip estacional, les persones recuperades poden perdre la immunitat i ser susceptibles de tornar a emmalaltir.

El desenvolupament dels models té dues fases, la primera d’ajust o entrenament i la segona de predicció. A la primera es determina la funció o model matemàtic i els valors dels paràmetres que són compatibles amb les dades que s’observen amb l’evolució de l’epidèmia (enfocament bayesià).

Una vegada que es té el model que s’ajusta millor a les dades, es passa a la segona fase, la de predicció. El problema, en algunes ocasions, com en aquesta pandèmia, ha estat la manca de dades. Els primers mesos de la pandèmia es desconeixia el nombre real d’infectats, de manera que la incertesa era molt alta. No obstant això, a mesura que s’han anat obtenint dades, els models matemàtics ens han ajudat a entendre com es desenvolupa aquesta epidèmia i a dissenyar estratègies per controlar-la d’una manera eficaç.

Saber com desapareix per esbrinar com va aparèixer

Els models que hem descrit a l’apartat anterior poden ser útils per a predir l’evolució de la malaltia, però no per a rastrejar l’aparició del primer cas. Per tal d’assolir aquest objectiu, els investigadors del nostre article han emprat de manera innovadora un model matemàtic desenvolupat per a l’extinció d’espècies.

Originalment el model ajuda a predir quan desapareixerà una espècie basant-se en el nombre d’organismes detectats. Però en aquest cas s’ha emprat un enfocament hàbil. El model s’ha invertit de manera que funciona en la direcció contrària per arribar al primer cas, tenint en compte aquells que es van detectar més tard i fins i tot aquells que van passar desapercebuts al començament.

Les conclusions d’aquest article coincideixen amb les d’uns altres estudis publicats prèviament: els autors tornen a indicar la data del 17 de novembre de 2019 a la qual fèiem referència abans.

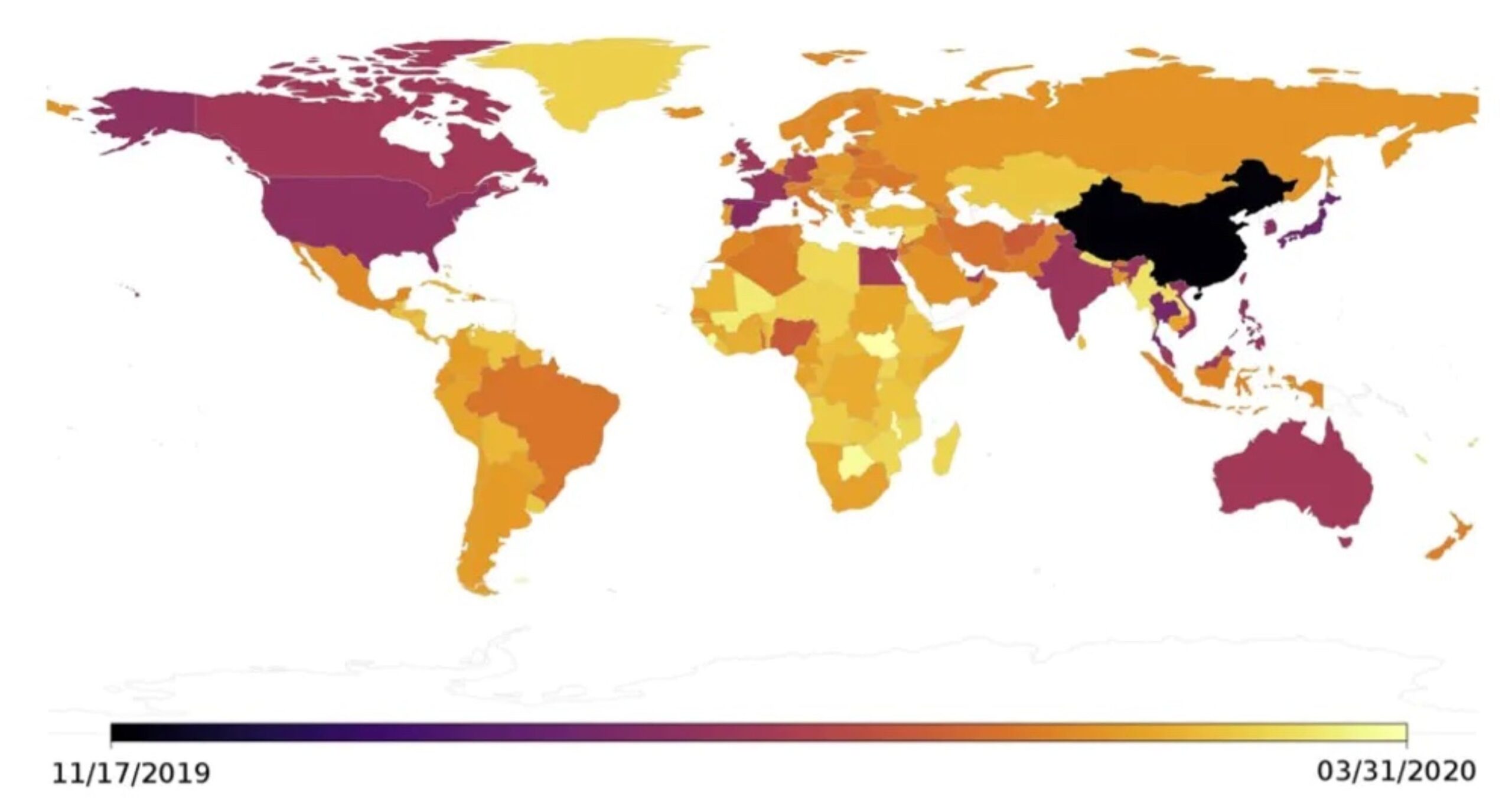
Si tenen raó, quan l’OMS va reaccionar a final de gener del 2020, la infecció es trobava ja a mig món. La Figura 2 mostra una aproximació temporal de com la pandèmia es va anar estenent. L’epidèmia va sorgir abans que no s’havia estimat i també es va transmetre més de pressa que no ens pensàvem.

Hi ha dos factors que van poder-hi influir: (1) es desconeixia la transmissió entre individus asimptomàtics i (2) es desconeixia la transmissió per aerosols. Com hem comentat, faltaven dades.

Tot convergeix el novembre del 2019

El fet que tant les investigacions sobre casos concrets com un model matemàtic indiquin una data determinada per a l’aparició del primer cas de covid-19 és molt encoratjador i ens indica que anem pel bon camí en aquesta investigació detectivesca.

Una possible debilitat del model podria ser l’existència d’alguna mena de biaix a l’hora de detectar els casos a l’inici de la pandèmia, sobretot en tractar-se d’un sol país. Potser en el futur es pugui obtenir més informació, o crear un model que tingui en compte aquest aspecte. O potser realment ja hem donat amb el cas original.

En qualsevol cas, després de l’enrenou creat per la crisi sanitària, ara ja albirem l’etapa en què mirarem enrere amb més tranquil·litat i podrem escriure la història de la pandèmia.